Efecto del distanciamiento social y la densidad de población en el combate contra el Coronavirus (COVID-19)

Recientemente me he encontrado trabajando en un modelo de epidemias en el que incluyo características como la distribución geográfica de la población. Aunque el modelo y los datos aún se encuentran en una fase muy temprana para hacer cualquier tipo de predicción, algunos de sus resultados tienen un valor de divulgación para hacer conciencia sobre la importancia del distanciamiento social para mitigar el número de casos del nuevo Coronavirus (COVID-19).

Debido a nuestra falta de intuición sobre el significado de un crecimiento exponencial en el número de casos, puede ser difícil apreciar la importancia de acciones como la auto-cuarentena. Es por ello que, con el propósito de generar mayor conciencia al respecto, me parece adecuado presentar algunas simulaciones visuales de como afecta la interacción de la población en el número de casos (infecciones) que se presentará a futuro.

En la presente simulación (reproducir el video), se genera una población inicial de individuos infectados (distribuidos aleatoriamente), los cuales tienen una probabilidad de infectar a los individuos con los que interactúan. A su vez, estos nuevos infectados podrán hacer lo mismo con el transcurso de los días, hasta que se recuperen y ya no representen una fuente de infección. La interacción de los individuos infectados con el resto de la población es a nivel local, pero ocasionalmente algunos se movilizan a otras zonas de la población.

Se asume que individuos ya curados no se infectan nuevamente y no se modelan las muertes, ya que la intensión es modelar el número de infecciones. El modelo también toma en cuenta factores como la densidad y distribución geográfica de la población, y se simula una disminución en la tasa de movilidad/interacción de la población al pasar del tiempo, para así tomar en cuenta el cambio de comportamiento de la población al aumentar su nivel de alerta.

En el primer caso tenemos una población distribuida aleatoriamente (gráfica izquierda) y de manera uniforme, en la que aparecen 5 individuos infectados (puntos rojos). Con el pasar de los días, estos individuos interactúan con otros (movimiento de los puntos) e infectan a una parte de los individuos con los que interactuaron, creando nuevos infectados. Después de 15 días aparecen los primeros individuos recuperados (puntos azules) , los cuales ya no infectarán a otros, aunque ya existe un reservorio suficiente de nuevos infectados. En la gráfica de la derecha se observa la evolución del número de casos por día.

En la siguiente simulación, la gráfica presenta una población con exactamente las mismas características, pero con una distribución geográfica más centralizada, es decir, mayor densidad de población al centro, y menor a las afueras, como ocurriría en una ciudad.

A pesar de que el único cambio en la simulación es la distribución de la población, el número de infectados crece mucho más rápido, observando un crecimiento exponencial en el número de casos por día ( gráfica a la derecha). De tal manera que en este tipo de poblaciones el distanciamiento social es de gran relevancia.

Si la movilidad/interacción de la población es reducida a un octavo (⅛), se observa el efecto en el número de casos simultáneos, donde el máximo valor es del 37% de la población que no redujo su movilidad/interacción, lo cual puede ser clave para evitar la saturación de los sistemas de salud de esa población.

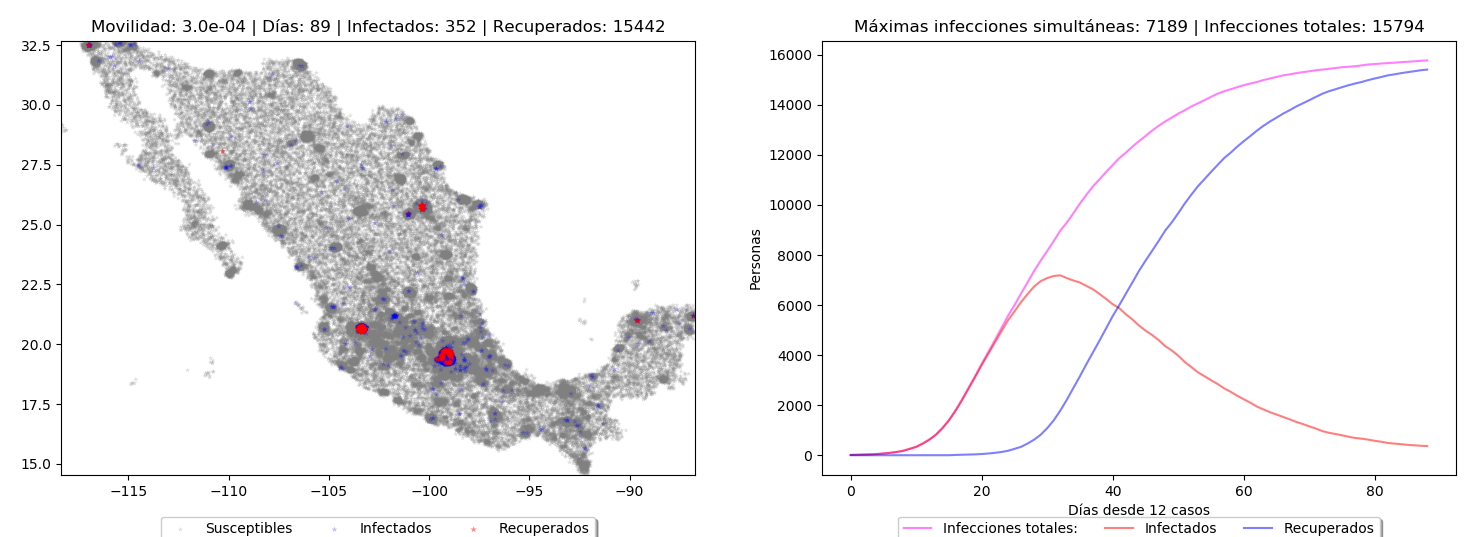
Dado que se ha visto la importancia de la distribución geográfica y la densidad de una población con respecto al número de casos que se presentarán, ¿Cómo podrían afectar estas características a México? En la siguiente animación se muestra una simulación del posible efecto en la población al considerar 12 infecciones iniciales, distribuidas aleatoriamente a lo largo del país. Aunque los parámetros del modelo se han ajustado para tratar de reproducir el numero de infecciones que se han reportado en México, el comportamiento futuro podría variar considerablemente.

 

Se observa claramente como con el paso del tiempo las ciudades más centralizadas y con mayor población tienden a aumentar rápidamente el número de casos presentados, por lo que es en estas zonas donde el distanciamiento social es de gran importancia.

Aunque en esta simulación la población reduce su movilidad conforme avanza el número de infecciones, la acción temprana producirá el mayor impacto sobre el máximo de casos simultáneos que se tendrán que afrontar.

 
 
  Insights:

• El distanciamiento social es clave para prevenir que el número de casos simultáneos crezca desproporcionadamente.
• Incluso con igual movilidad, extensión territorial y número de individuos, las poblaciones que tiene zonas con una alta concentración de individuos, como es el caso de las ciudades, se verán más afectadas, por lo que es en estas poblaciones donde debe haber más conciencia sobre el efecto de su comportamiento.